A convex set is a Set of vectors that contains all line segments between vectors in the set. Consider the following shape:
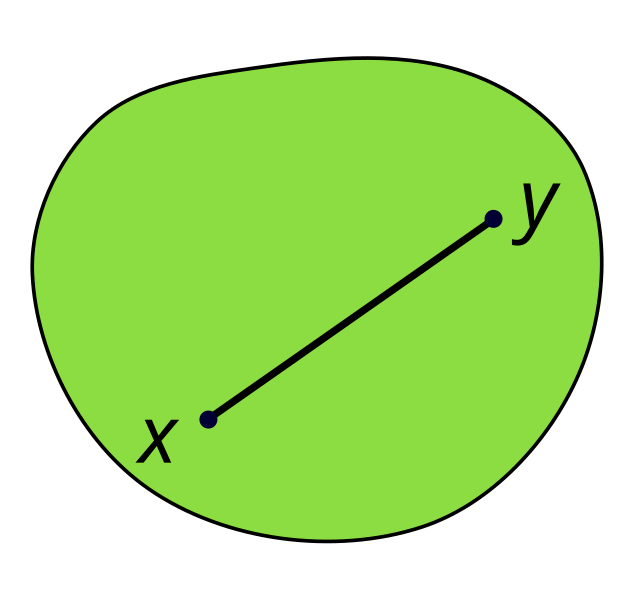
As shown, a line segment between two points $~$x$~$ and $~$y$~$ in this shape lies entirely within the shape. In fact, this is true for any pair of points in the shape. Therefore, this shape is convex. For comparison, the following shape is not convex:
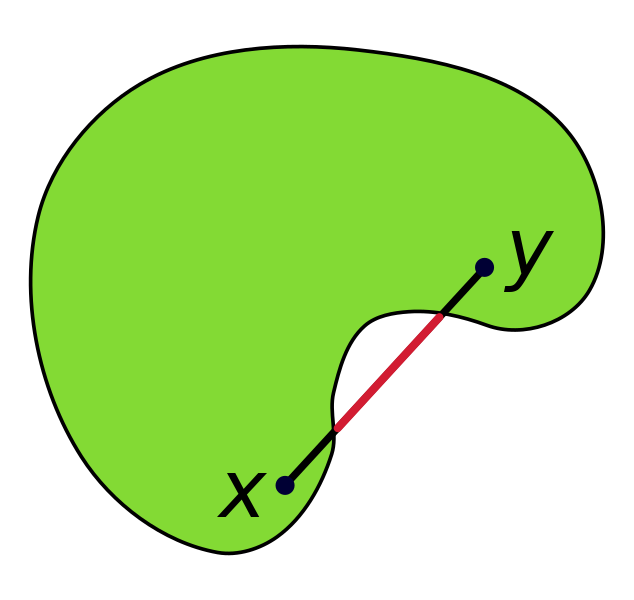
The fact that part of the line segment between $~$x$~$ and $~$y$~$ (both inside the shape) lies outside the shape proves that this shape is not convex.
Formally, a set $~$S$~$ is convex if
$$~$\forall x, y \in S, \theta \in [0, 1]: \theta x + (1 - \theta) y \in S$~$$
(images are from Wikipedia: here and here)
[todo: use non-Wikipedia images and remove the attribution]